一、本文介绍

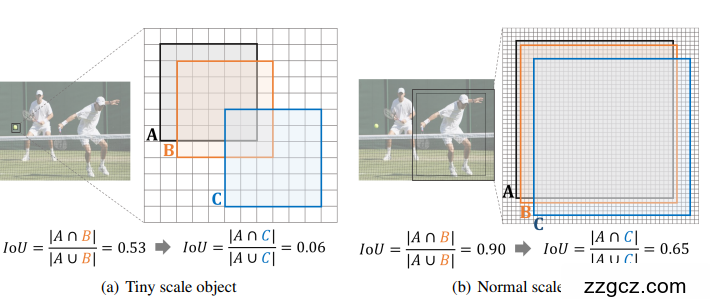
本文记录的是 基于NWD的RT-DETR的损失函数改进方法研究 。目前的IoU-Loss在一些情况下不能提供梯度来优化网络，例如当预测边界框P和真实边界框G没有重叠（即 $|P\cap G|=0$ ），或者P完全包含G或反之（即 $|P\cap G|=P$ 或G），而这两种情况在微小物体检测中非常常见。 CIoU 和 DIoU 虽然能处理上述两种情况，但它们基于IoU， 对微小物体的位置偏差很敏感 。而 本文的改进方法能够使模型解决这些问题，实现对小目标的精确检测 。

---

---

二、NWD设计原理

NWD损失函数 设计的原理及优势如下：

2.1 NWD计算原理

• 首先将边界框建模为二维高斯分布，对于两个二维高斯分布 $m{u}_1=N(m_1,{\sum }_1)$ 和 ${\mu }_2=N(m_2,{\sum }_2)$ ，其二阶Wasserstein距离定义为： $W_2^2({\mu }_1,{\mu }_2)=\parallel m_1-m_2{\parallel }_2^2+Tr({\sum }_1+{\sum }_2-2({\sum }_2^{\frac{1}{2}}{\sum }_1{\sum }_2^{\frac{1}{2}}{)}^{\frac{1}{2}})$ ，可简化为： $W_2^2({\mu }_1,{\mu }_2)=\parallel m_1-m_2{\parallel }_2^2+\parallel {\sum }_1^{\frac{1}{2}}-{\sum }_2^{\frac{1}{2}}{\parallel }_F^2$ 。
• 对于从边界框A = $(c{x}_a,c{y}_a,w_a,h_a)$ 和B = $(c{x}_b,c{y}_b,w_b,h_b)$ 建模的高斯分布 $N_a$ 和 $N_b$ ，可进一步简化为： $W_2^2({\mathcal{N}}_a,{\mathcal{N}}_b)=\parallel ([c{x}_a,c{y}_a,\frac{w_a}{2},\frac{h_a}{2}{]}^T,[c{x}_b,c{y}_b,\frac{w_b}{2},\frac{h_b}{2}{]}^T){\parallel }_2^2$ 。
• $W_2^2({\mathcal{N}}_a,{\mathcal{N}}_b)$ 是距离度量，不能直接用作相似度量（即像IoU一样的值在0和1之间），所以使用其指数形式归一化，得到新的度量NWD： $NWD({\mathcal{N}}_a,{\mathcal{N}}_b)=exp(-\frac{\sqrt{W_2^2({\mathcal{N}}_a,{\mathcal{N}}_b)}}{C})$ ，其中C是一个与数据集密切相关的常数，在实验中经验性地设置为AI - TOD的平均绝对大小，并取得了最佳性能，且在一定范围内是稳健的。
• NWD损失函数 设计为： ${\mathcal{L}}_{NWD}=1-NWD({\mathcal{N}}_p,{\mathcal{N}}_g)$ ，其中 $N_p$ 是预测框P的高斯分布模型， $N_g$ 是真实边界框G的高斯分布模型。

2.2 NWD优势

• 尺度不变性 ：与IoU相比， NWD 对边界框的尺度变化不敏感，更适合测量微小物体之间的相似性。
• 对位置偏差的平滑性 ：IoU对微小物体的位置偏差过于敏感，而 NWD 因位置偏差产生的变化更平滑，这表明在相同阈值下， NWD 有可能比IoU更好地区分正/负样本。
• 能测量非重叠或相互包含边界框的相似性 ：即使边界框没有重叠或重叠可忽略， NWD 也能测量它们之间的分布相似性。
• 提供梯度 ：根据上述介绍， NWD损失函数 在 $|P\cap G|=0$ 和 $P\cap G|=P$ 或G的情况下都能提供梯度。

论文： https://arxiv.org/pdf/2110.13389
源码： https://github.com/jwwangchn/NWD

---

三、NWD的实现代码

NWD 的实现代码如下：

def wasserstein_loss(pred, target, eps=1e-7, constant=12.8):
    r"""`Implementation of paper `Enhancing Geometric Factors into
    Model Learning and Inference for Object Detection and Instance
    Segmentation <https://arxiv.org/abs/2005.03572>`_.
    Code is modified from https://github.com/Zzh-tju/CIoU.
    Args:
        pred (Tensor): Predicted bboxes of format (x_center, y_center, w, h),
            shape (n, 4).
        target (Tensor): Corresponding gt bboxes, shape (n, 4).
        eps (float): Eps to avoid log(0).
    Return:
        Tensor: Loss tensor.
    """

    center1 = pred[:, :2]
    center2 = target[:, :2]

    whs = center1[:, :2] - center2[:, :2]

    center_distance = whs[:, 0] * whs[:, 0] + whs[:, 1] * whs[:, 1] + eps #

    w1 = pred[:, 2]  + eps
    h1 = pred[:, 3]  + eps
    w2 = target[:, 2] + eps
    h2 = target[:, 3] + eps

    wh_distance = ((w1 - w2) ** 2 + (h1 - h2) ** 2) / 4

    wasserstein_2 = center_distance + wh_distance
    return torch.exp(-torch.sqrt(wasserstein_2) / constant)

---

四、添加步骤

4.1 修改ultralytics/utils/metrics.py

此处需要查看的文件是 ultralytics/utils/metrics.py

metrics.py 中定义了模型的损失函数和计算方法，我们想要加入新的损失函数就只需要将代码放到这个文件内即可

NWD 添加后如下：

4.2 修改ultralytics/utils/loss.py

在 ultralytics/utils/loss.py 在的引用中添加 wasserstein_loss ，然后在 BboxLoss函数 中修改如下代码，使模型调用此 wasserstein_loss 损失函数。

iou = bbox_iou(pred_bboxes[fg_mask], target_bboxes[fg_mask], xywh=False, CIoU=True)

loss_iou = ((1.0 - iou) * weight).sum() / target_scores_sum

在上方代码下方添加如下代码：

nwd = wasserstein_loss(pred_bboxes[fg_mask], target_bboxes[fg_mask])
iou_ratio = 0.3  #可调超参数，小目标可变低
nwd_loss = ((1.0 - nwd) * weight).sum() / target_scores_sum
loss_iou = iou_ratio * loss_iou + (1 - iou_ratio) * nwd_loss

此时再次训练模型便会使用 NWD 计算模型的损失函数。

---

五、成功运行截图