困惑度（Perplexity）在固定长度模型中的应用¶

什么是困惑度？¶

困惑度（PPL）是评估语言模型性能最常用的指标之一。需要注意的是，这个指标主要用于传统的自回归（或因果）语言模型，而对于像 BERT 这样的掩码语言模型则不太适用（详见模型总结）。

困惑度的定义是对序列的平均负对数似然取指数。如果有分词后的序列 $X = (x_0, x_1, \dots, x_t)$，那么该序列的困惑度 PPL(X) 通过以下公式计算： $$ \text{PPL}(X) = \exp \left\{ -\frac{1}{t}\sum_{i=1}^t \log p_\theta (x_i|x_{<i}) \right\} $$ 其中，$\log p_\theta (x_i|x_{<i})$ 是根据模型计算的第 $i$ 个词在其前面的词条件下的对数似然。直观上，困惑度可以评估模型在给定语料库中对指定词汇的预测均匀性。需要注意的是，分词方式会直接影响模型的困惑度，因此在比较不同模型时应始终考虑这一点。

困惑度也等价于数据与模型预测之间的交叉熵的指数。有关困惑度及其与每字符比特数（BPC）和数据压缩关系的更深入理解，可以参考这篇博客文章。

使用固定长度模型计算困惑度¶

如果我们不受模型上下文大小的限制，可以对整个序列进行自回归分解，每次预测时都以前面所有词为条件。

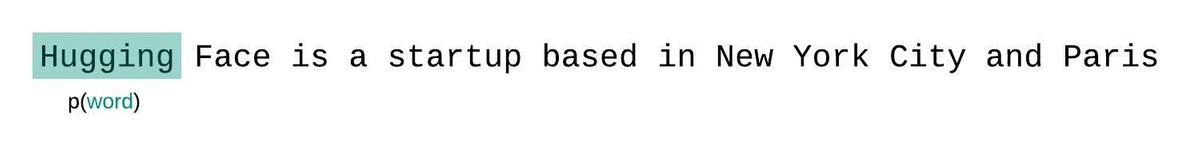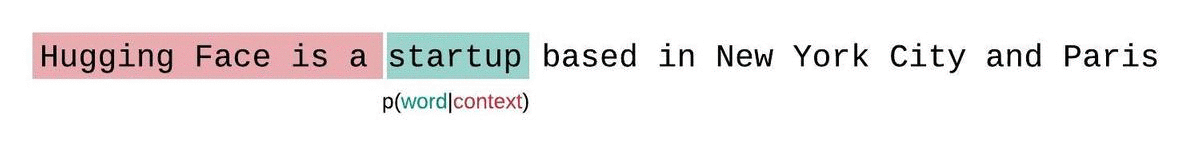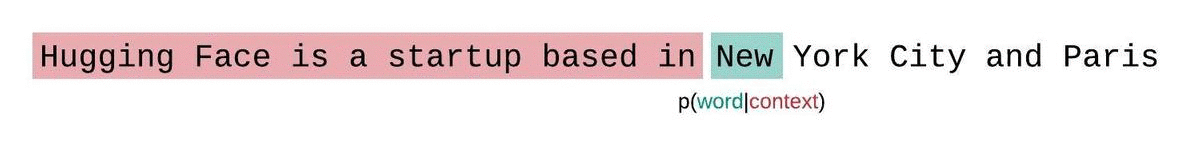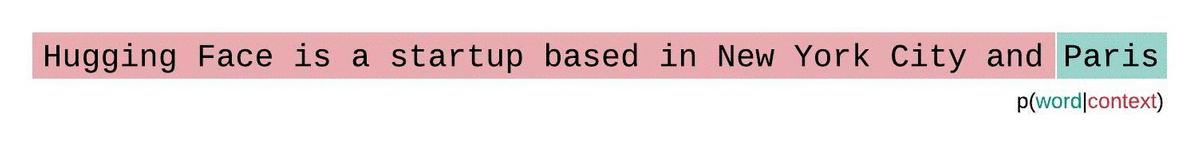
但在实际应用中，我们通常会受到模型处理的令牌数量的限制。例如，GPT-2 的最大上下文长度为 1024 个令牌，因此当 $t>1024$ 时，我们无法直接计算 $p_\theta(x_t|x_{<t})$。

为了应对这种情况，通常将序列分割成与模型最大输入长度相等的子序列。如果模型的最大输入长度为 $k$，那么我们只需考虑每个令牌前面的 $k−1$ 个令牌，而不是整个上下文。计算模型困惑度时，一个简单但次优的方法是将序列分解为不重叠的片段，并独立计算每个片段的对数似然。

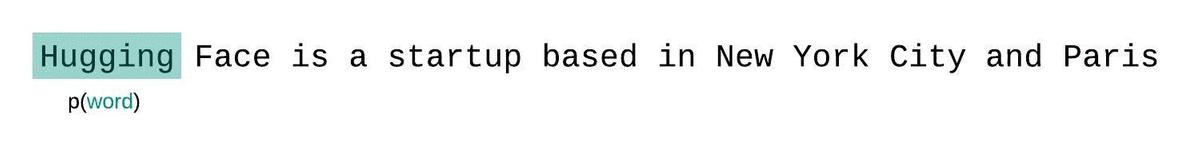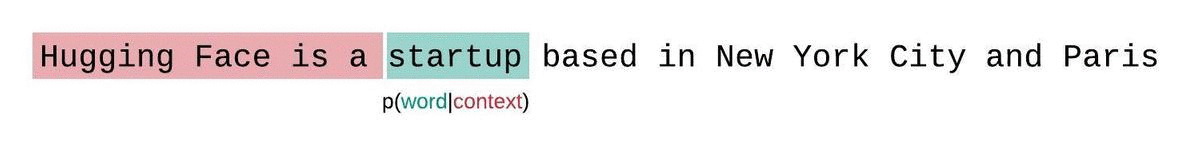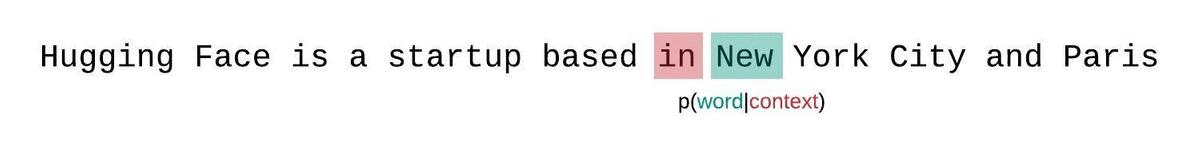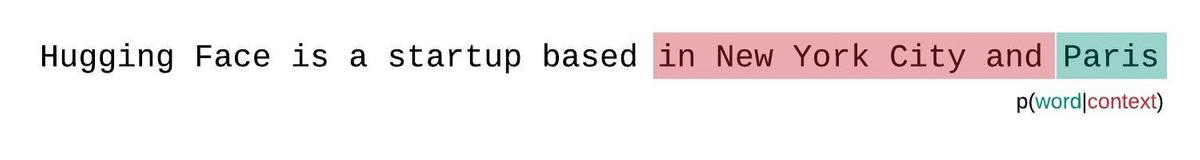
这种方法的优点是计算速度快，但作为完全分解困惑度的近似效果较差，通常会得到更高的（更差的）困惑度，因为模型在大多数预测步骤中会有更少的上下文。

更好的方法是使用滑动窗口策略。通过不断滑动上下文窗口，使模型在每次预测时都能获得更多的上下文。

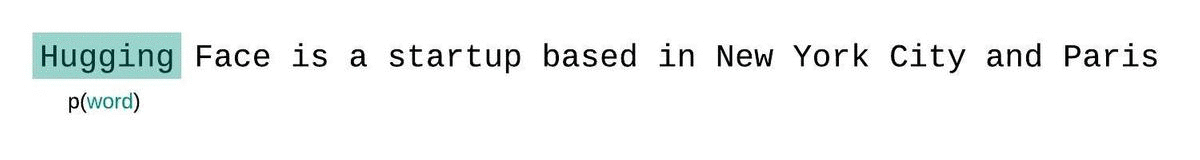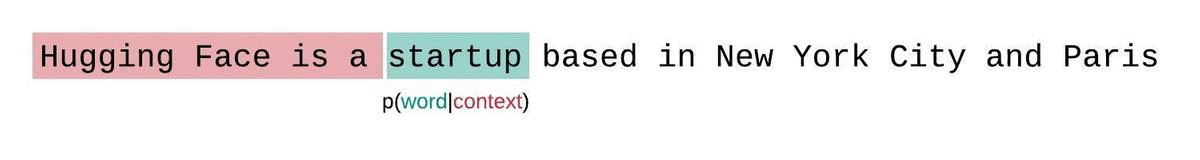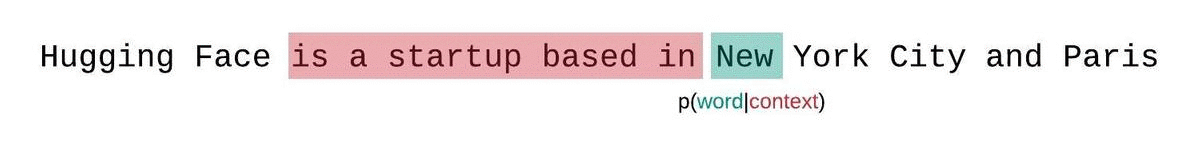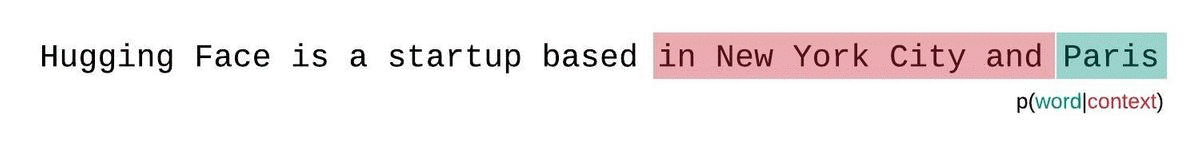
这种方法更接近真实序列概率的分解，通常会产生更优的结果。缺点是需要为语料库中的每个令牌进行一次前向计算。一种实用的折中方法是采用步长较大的滑动窗口，而不是每次只滑动一个令牌。这可以在保持较大上下文的同时提高计算速度。

示例：使用 🤗 Transformers 和 GPT-2 计算困惑度¶

让我们用 GPT-2 来演示这个过程。